题目:平衡二叉树
思路:
返回值:层数
终止条件:如果root == nullptr
单层循环逻辑:判断左右子树的返回值是否为-1,若为-1说明此树已经不是平衡二叉树了,若值不为-1则需要判断最后子树的返回值是否相差大于1,若大于1则返回-1,若小于1则返回本层的高度。
本体采用的是后序遍历的方式
class Solution {
public:
int couthigh(TreeNode* root)
{
if(root == nullptr) return 0;
int left = couthigh(root->left);
int right = couthigh(root->right);
if(left == -1 || right == -1) return -1;
if(abs(right - left) > 1) return -1;
return max(left,right)+ 1;
}
bool isBalanced(TreeNode* root) {
int i = couthigh(root);
if(i == -1) return false;
return true;
}
};题目:二叉树的所有路径
思路:用前序的方式可以做
注意:中的位置一定要放在最上面,否则最后一个值可能会保存不到路径中而导致回溯过程中出错
class Solution {
public:
void traversal(TreeNode* root, vector<int>&cur ,vector<string>&result)
{
cur.push_back(root->val); // 中
if(root->left == nullptr && root->right == nullptr)
{
string tmp;
for(int i = 0; i < cur.size() - 1; i++)
{
tmp += to_string(cur[i]);
tmp += "->";
}
tmp += to_string(cur[cur.size() - 1]);
result.push_back(tmp);
return;
}
if(root->left != nullptr) // 左
{
traversal(root->left,cur,result);
cur.pop_back();
}
if(root->right != nullptr) //右
{
traversal(root->right,cur,result);
cur.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<int> cur;
vector<string> result;
traversal(root,cur,result);
return result;
}
};题目:左叶子之和
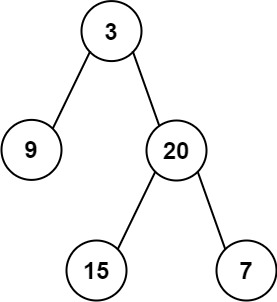
思路:这道题目我自己做题容易混淆的一个点是将if(root ->left != nullptr && root->left->left == nullptr && root->left->right == nullptr)这个判断作为终止条件,但是这样左会出现一个错误,就像下面图中的内容,若将其作为终止条件会导致第一个递归就会导致递归进程的结束。
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if(root == nullptr)
{
return 0;
}
if(root->left == nullptr && root->right == nullptr)
{
return 0;
}
int left = sumOfLeftLeaves(root->left);
if(root ->left != nullptr && root->left->left == nullptr && root->left->right == nullptr)
{
left = root->left->val;
}
int right = sumOfLeftLeaves(root->right);
return left + right;
}
};题目:完全二叉树的节点个数
222. 完全二叉树的节点个数 - 力扣(LeetCode)
思路:
返回值:节点个数
终止条件:节点为空节点
单层逻辑:将左右子树的节点相加后+1 返回此树的节点个数给上传
遍历顺序:后序
class Solution {
public:
int countNodes(TreeNode* root) {
if(root == nullptr) return 0;
int left = countNodes(root->left);
int right = countNodes(root->right);
return left+ right + 1;
}
};
评论