题目:找树左下角的值
递归思路:
返回值:null
终止条件:是否为根节点,若为根节点则返回值
单层逻辑:分别从左子树和右子树进行向下的搜索,从而计算每个节点的高度,协助找到左下角的值,注意每层需要回溯。
class Solution {
public:
int result = 0;
int max_depth = INT_MIN;
void traversal(TreeNode* root, int depth)
{
if(root->left == nullptr && root->right == nullptr)
{
if(depth > max_depth)
{
result = root->val;
max_depth = depth;
}
}
if(root->left != nullptr) //确保终止条件不会报错
{
depth++;
traversal(root->left,depth);
depth--; //回溯
}
if(root->right != nullptr)
{
depth ++;
traversal(root->right,depth);
depth --;//回溯
}
}
int findBottomLeftValue(TreeNode* root) {
int depth = 1;
traversal(root,depth);
return result;
}
};层序法:相对比较好理解,自己直接写了一遍,一次AC。
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
vector<vector<int>> nums;
queue<TreeNode*> que;
que.push(root);
while(!que.empty())
{
int size = que.size();
vector<int> one;
for(int i = 0; i < size;i++)
{
TreeNode* node = que.front();
que.pop();
one.push_back(node->val);
if(node->left != nullptr)
{
que.push(node->left);
}
if(node->right != nullptr)
{
que.push(node->right);
}
}
nums.push_back(one);
}
return nums[nums.size()-1][0];
}
};题目:路径总和
思路:还是使用递归的逻辑,和二叉树的所有路径题目极其相似,两题都需要回溯来进行操作。
代码:
class Solution {
public:
bool istrue = false;
void traversal(TreeNode* root,int targetSum,int sums)
{
if(root->left == nullptr && root->right == nullptr)
{
if(sums == targetSum)
{
istrue = true;
}
}
if(root->left != nullptr)
{
sums += root->left->val;
traversal(root->left,targetSum, sums);
sums -= root->left->val;
}
if(root->right != nullptr)
{
sums += root->right->val;
traversal(root->right,targetSum, sums);
sums -= root->right->val;
}
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
{
return false;
}
int sums = root->val; //初始化第一个节点的值,因为这个值在上面的遍历过程中不会被加入sums中
traversal(root,targetSum,sums);
return istrue;
}
};题目:从中序与后序遍历序列构造二叉树(二刷没刷出来的题目)
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
本体的难点是:
如何通过中序与后序找到左右子树的值
如何用递归来进行单层递归的逻辑
在此处引用代码随想录中的图片来帮助理解
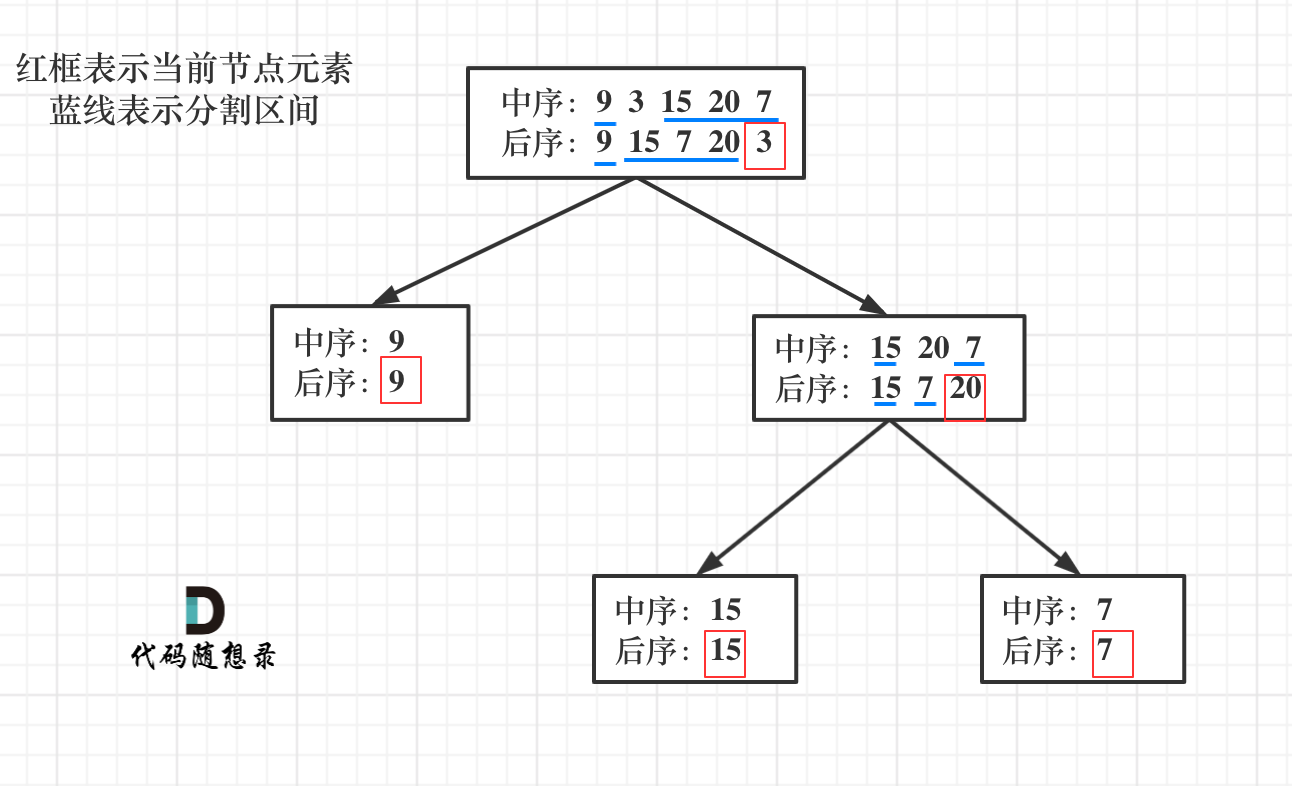
我们需要根据后续的末尾字符来判断中间节点的值,再一句中间节点的值来判断中序中左右子树的值。
单层递归逻辑:(我们需要在每一层创建子树来返回给上层)
找到中节点的位置
创建中节点
基于中节点分割前序的左右子树,依据分割好的前序左子树的大小来分割后续的左右子树(注意前序和后续分割后的左子树和右子树的值是相同的但是因为遍历方式不同因此顺序是不同的)
使用递归的方式处理左子树和右子树
class Solution {
public:
TreeNode* traversal(vector<int>&inorder , vector<int>&postorder)
{
if(postorder.size() == 0)
{
return nullptr;
}
//找到后序遍历的中,
int mid = postorder[postorder.size()-1];
//创建节点
TreeNode* mid_node = new TreeNode(mid);
if(postorder.size() == 1)
{
return mid_node;
}
//根据中间节点进行分割中序
int delimiterIndex;
for(delimiterIndex = 0; delimiterIndex< inorder.size();delimiterIndex++)
{
if(inorder[delimiterIndex] == mid)
{
break;
}
}
//分割前序 左闭右开区间:[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(),inorder.begin() + delimiterIndex);
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());
// postorder 舍弃末尾元素
postorder.resize(postorder.size() -1);
//分割后续
vector<int> leftPostorder(postorder.begin(),postorder.begin()+ leftInorder.size());
vector<int> rightPostorder(postorder.begin()+ leftInorder.size(), postorder.end());
mid_node->left = traversal(leftInorder,leftPostorder);
mid_node->right = traversal(rightInorder,rightPostorder);
return mid_node;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return traversal(inorder,postorder);
}
};加练题:从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
题目:给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。

示例:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]这道题目和上面的题目是相同相差不大,需要用前序来找到中节点的位置,其过程如下

class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size()== 0)
{
return nullptr;
}
//找到中节点
int mid = preorder[0];
TreeNode* mid_node = new TreeNode(mid);
if(preorder.size() == 1)
{
return mid_node;
}
int mid_index;
for(mid_index = 0;mid_index < inorder.size();mid_index++)
{
if(inorder[mid_index] == mid)
{
break;
}
}
//分割
vector<int> leftInorder(inorder.begin(),inorder.begin() + mid_index);
vector<int> rightInorder(inorder.begin() + mid_index+1,inorder.end());
vector<int> leftpreorder(preorder.begin()+1,preorder.begin()+1+leftInorder.size());
vector<int> rightpreorder(preorder.begin()+1+leftInorder.size(),preorder.end());
mid_node->left = buildTree(leftpreorder,leftInorder);
mid_node->right = buildTree(rightpreorder,rightInorder);
return mid_node;
}
};
评论